Strength in Learning: A Learner’s Conference

Written by: Berniece Gowan

Literacy Alberta’s Strength in Learning: A Learner’s Conference took place on the Bow Valley College campus, Saturday April 5/2014.

Gail McDougal, Literacy Coordinator for Calgary John Howard, is Literacy Alberta’s lead for this project. This was a free event and included workshops, materials, lunch/snacks for all registered attendees.

The Centre for Excellence in Foundational Learning/Bow Valley College supported this event through assistance with planning, marketing, event and classroom space bookings and coordinating IT support. There was a display area with materials from Calgary John Howard(CJH), Literacy Alberta and Mount Royal University. The learners and tutors came from programs at the Calgary Public Library, Calgary John Howard, Bow Valley College and Mount Royal University.

The keynote speaker for the day was Michelle Cameron-Coulter. Michelle was a warm and inspiring speaker, encouraging us to embrace our possibilities, to risk changing and becoming more of who we want to be.

The event was hosted by Roger Hendrickson, recipient of Calgary Learns 2013 ‘Adult Learner’ Life of Learning Award (LOLA). Roger, a former learner from CJH, has been an inspiration in the adult learning community as he speaks out about his  life and his literacy journey.

One of the goals of this conference was to provide learners (and tutors) with fun and engaging ways to strengthen their learning. Students and tutors had a number of workshops to choose from. Literacy Alberta staff facilitated workshops on True Colors, Career Planning and Learning Abilities. The Calgary Public Library delivered a workshop about Online Learning and also provided an orientation to Library services. Momentum and  Vecova delivered workshops on assets and financial literacy/financial management.

April 5 was also our first brilliant spring day! Although the number of delegates was lower than expected, feedback from the day was very positive.

Thank you to BVC faculty, staff and students for supporting this event.

Nations Learning Together Blog Launch Party

On April 4, CEFL held a launch party for the Nations Learning Together blog at Bow Valley College. The launch was a celebration of blog posts involving poems, artwork, and short stories created by learners from Lifeline to Literacy, Speech-Assisted Reading and Writing (SARAW), Adult Basic Literacy Education (ABLE), Artstream, Life Management (Calgary Remand Centre), and the Aboriginal Upgrading program. The event was an opportunity to share the work of students and learn about the history of the Nations Learning Together project. Audriana Monteiro, a University of Calgary practicum student who worked with SARAW and ABLE, presented her experience of working on the blog with learners. She described the significance of sharing work and making connections to people through blogging. As well, ABLE students read their work from the blog and instructors shared their thoughts and experience of the project.

Thank you to the CEFL students and staff that came out to support the launch. Thanks also to Belle Auld, Carol McCullough, and Audriana Monteiro for putting the event together.

Click here to view the blog.

Carol McCullough, ABLE Instructor hosted the launch event.

Nations Learning Together blog on display.

Samra Admasu, ALRI Communication Officer

Debra King, Lifeline to Literacy Instructor

Sheri Lockwood, Life Management Instructor

Audriana Monteiro, University of Calgary Practicum Student 

Nations Learning Together Blog. 

Presentation on blogging and the impact on learners.

Carol and Belle presented a thank you gift to Audriana for her contribution to SARAW and ABLE.

U of C Student Teachers Return to CEFL - Lorna Malanik

     For the first time in over a decade and a half, the Centre for Excellence in Foundational Learning hosted student-teachers.  In the second practicum of their first year, student-teachers are required to experience alternative, small group delivery and so five excited potential teachers were paired with FlexClass instructors for three weeks.

    
 The instructors in FlexClass feel that our student-teachers were very lucky to have been chosen to do their practicum with Bow Valley College.   We are very proud of what we do in the CEFL and to be able to provide these new teachers with experiences that are unique and leading edge.  The three weeks went very quickly as each student-teacher experienced not only the FlexClass class environment, but also got to sit in on RTOL classes, be shown ATOL, participate in a smudge ceremony  at the Iniikokaan Aboriginal Centre, and be involved in an exam review session. The students also made small group presentations and worked with FlexClass students one-on-one. 

     
Over the three weeks that the student-teachers were with us, they gained a deep appreciation for what ‘diversity in the classroom’ really means.  It was interesting for the student-teachers to meet learners with such unique backgrounds, varied ages, and dissimilar educational experiences returning to school for a multitude of reasons and with a range of goals upon finishing.  The student-teachers commented on the level of commitment required of a student returning to school – often juggling work, children, and other obligations all while fulfilling their study requirements and ultimately bettering their own lives and the lives of their families.  Over the three weeks, the practicum students gained a renewed respect for what it means to be a life-long learner and also solidified the importance of becoming skilled and knowledgeable teachers themselves in order to help young learners gain a solid foundation in their early years. 

     
In the words of the practicum students:

"Being a part of the BVC staff and instructors for the past three weeks has been an eye opening experience for all of us. We have learned much about adult learners and their needs through our partner teachers and we are extremely grateful for this opportunity. Working with such focused and motivated students gave us a deeper insight on the type of environment BVC offers. The level  of devotion and professionalism among the BVC staff has made us work harder and strive to be the best teachers we can be in our near future.  Students at BVC are quite different than the students we see in traditional high schools. These students came to BVC because they wanted to, not because they had to. They are motivated and deserve
all the credit for being successful. Having the confidence to trust yourself to complete a course shows how dedicated the students and their instructors are. We are humbled by this experience  and hope to carry this level of devotion in our future careers as teachers.”

     It was a pleasure to re-experience teaching through fresh eyes and to see the growth our student-teachers experienced in a mere three weeks.  Thank you to all instructors and staff who welcomed the student-teachers to the College as well as your classrooms; your efforts made this an enriching experience for all.  We look forward to welcoming a new set of student-teachers in the near future.

Mental Mathematics Workshop Presented by Rosalind Carson

On March 10th, 2014, I attended the  “Mental Mathematics” workshop presented by Rosalind Carson.

Rosalind explained why mental mathematics even in this age of ubiquitous computers and cell phones is still a useful skill.  A few examples:  Fibre optics installers deal with multiples of 12 and perform complex addition without the use calculators because both their hands are required to hold cables as they work; skilled accountants perform complex calculations in their minds when meeting with clients, often as a demonstration of accounting prowess.

While renovating my basement, I noticed that the original framer (circa 1968) performed the short Continental method of division (see an example at http://www.csus.edu/indiv/o/oreyd/acp.htm_files/cerme.portugal.div.jpg) in pencil on the 2x4s that were eventually installed.  Only the minuend is written down.  The subtrahend (the number taken from the minuend) is kept in short term memory and the subtraction operation is performed entirely mentally.  Subtracting three-digit numbers mentally is feasible with practice, especially if you can at least see the minuend.   Much of the challenge of performing math operations mentally (no paper permitted) is the limitations of short-term memory, 7 digits plus or minus 2.  Many of the strategies Rosalind outlined are designed to reduce cognitive load, especially the burden placed on short-term memory.

There has been some controversy regarding fears that the Curriclum Redesign will in some way neglect mental mathematics:  http://www.theglobeandmail.com/news/national/education/alberta-education-reforms-ignore-kids-parents/article17390684/  .  However, I see no compelling indications that the Redesign will reduce mental mathematics or other foundational skills.  See http://www.edmontonjournal.com/Staples+Major+educational+changes+mean+fluffy+system+Education+minister+says/9615571/story.html for a sample of the ongoing controversy.  “We’re not moving to a fuzzy system of completely learner, self-guided system of education where the teacher is not actually a teacher, but they learn along with the student. I don’t know where that crap came from to tell you the truth.” says Minister Johnson, as quoted in the article.  I am not yet convinced that the redesign is excessively soft-hearted or insufficiently hard-headed, as some critics allege.  

Most of the techniques presented were drawn from Arthur Benjamin.  See http://www.amazon.ca/Secrets-Mental-Math-Mathemagicians-Calculation/dp/0307338401 for one of his books.  Dr. Arthur Benjamin’s Home Page:  http://www.math.hmc.edu/~benjamin/ .  Dr. Benjamin was a keynote presenter at MCATA 2010.

A targeted set of mental math skills is of use to many, but some are so arcane as to be mainly of academic interest.  For example, before electronic calculators were available, this skill had economic value:  “How to Multiply by a Mixed Number in Which the Fraction Is an Aliquot Part of the Rest of the Number, e.g., 20.2, 70.25, 80⅘, 75⅜, 625⅝…  “ (Meyers, 1967).   This section title is from a gem I found at a library’s discarded book sale, entitled High-Speed Math.  The library card still in the back shows that this book was never signed out: it languished for decades on its shelf unfriended.  Mechanical calculators were available in ‘67 but were still so cumbersome and expensive that calculating mentally was often more efficient.  Time was, this sort of easy facility with numbers was of premiere economic value.  No longer.  Easy facility with calculators and spreadsheets is often more valuable at present.  Nonetheless, understanding why these mental mathematics short-cuts work can reinforce an understanding of algebra, which is the level of abstraction the short-cuts are often based on.

The techniques that were introduced are certainly relevant to the curriculum: “A true sense of number goes well beyond the skills of simply counting, memorizing facts and the situational rote use of algorithms.  Students with strong number sense are able to judge the reasonableness of a solution, describe relationships between different types of numbers… to develop a deeper conceptual understanding of mathematics.” (Alberta Education, 2008, p.8).

Regards,

Michael

Previous blog postings

ELA 30-2 Equivalency Exam Project Completion

The Exam Development Team is delighted to share that the English Language Arts 30-2 Equivalency Exam Project is complete! This project has been underway for a little over a year. Thank you VERY much to all the exam reviewers and item writers who so generously gave their time and expertise to this project. 

Exam Reviewers and Item Writers:

Meghan Clayton

Susan Lemmer
Lorna Malanik

Tasha Nott

Patricia Pryce

Murray Ronaghan

Jennefer Rousseau

Chris Taylor

Congratulations to all on a job spectacularly well done! Thank you also to Carey Hilgartner, Karim Jaber, and Karlie Wimble for your continued support throughout the project. 

Please join me in thanking and congratulating the ELA 30-2 Equivalency Exam Review Project Team!

Susan Lemmer, Tasha Nott, Jennefer Rousseau, Murray Ronaghan, Lorna Malanik, Meghan Clayton, Chris Taylor
(not pictured: Patricia Pryce) 

An Easy Way to Estimate Unit Exam Reliability

Introduction

This article shows an easy way to estimate the reliability of selected-response (multiple-choice and numerical-response) tests by using Kudar and Richardson Fromula 21 (KR21).  This methodology is applied to Mathematics 30-1 Unit 1 Exam Form A and Form B.  A spreadsheet is provided that implements KR21 to easily estimate the reliability of a set of test scores.  The reliabilities of the scores produced by Form A and B are very high.  Colloquially, these exams could be said to be “very reliable exams.”  However, in truth, exams cannot be reliable: only the score sets they produce can be so.  This is because a certain exam may produce reliable results for one population, and yet produce quite unreliable results for another.  In this article, the on-campus and online populations are being treated as one population, under the assumption that both are very similar; however, I have no statistics to justify this.

Background

In 2012, I created four unit exams for Mathematics 30-1.  For a year, these were the only Mathematics 30-1 unit exams in existence in our department.  Since then, Debbie Scott has cloned them to produce Form B’s.  Were the Form A’s worthy of being cloned?  Are they cultivars with desirable characteristics? In Methodologies for Evaluating the Validity of Scores Produced by CEFL’s Equivalency Exams, I looked at the criterion-referenced validity of the unit exams by comparing class scores to diploma exam scores.  The criterion-referenced validity of the scores collectively produced by the unit exams is very high.  On a practical level, this means that the rank order of student performance on the unit exams is largely repeated on the diploma exam.  If the rank order of scores on the unit exams from lowest to highest is Vera, Chuck, and Dave (The Beatles, 1963), then the rank order of scores on the diploma exams will also likely be Vera, Chuck, and Dave.  Carefully propagating the form A Mathematics 30-1 unit exams will likely produce new forms that also produce valid scores--this on the assumption that the diploma exam is itself the most valid measure of ability in the course.  

In this article, I look at the reliabilities of individual unit exams (rather than the validities of the class scores) as a next step in building a validity argument that supports the validity of the scores they produce.

Kudar and Richardson Formula 21 (KR21)

This article investigates the reliability of Unit 1 Exam Form A and Unit 2 Exam Form A using a simple method.  Complex item-analysis software is not required to derive this statistic (however, item-analysis provides useful information about the reliability of individual items).  I employed Google Spreadsheets to estimate reliability using Kudar-Richardson Formula 21 (KR21):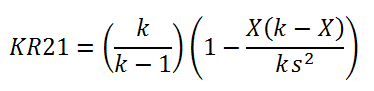

where k is the number of items on the exam, X is the mean of the raw scores, and s is the standard deviation of the raw scores.  Raw scores--not percentage scores--must be used to produce the statistics that are put into this formula.  Zeroes for students who missed the exam must not be included, else the reliability will be spuriously inflated.  This formula is easy to use because the only data we need are the students’ raw scores.  As long as the exam is entirely composed of selected-response items (multiple-choice or numerical-response items), then this formula will provide an estimate of the reliability statistic.  Scores on written-response items cannot be used because they are usually polytomously scored, i.e., they are not marked as entirely correct or entirely incorrect as selected-response items are.  And because KR12 always underestimates reliability, we can be confident that the true reliability is at least as large as the value produced by KR21.

Reliability and Validity

Violato (1992) provides some general guidelines for evaluating the reliabilities of teacher-made tests: 0.50 or greater is acceptable, and 0.70 or greater is excellent. Tests produced by professional testing agencies should have reliabilities of at least 0.80, which means that 80% of the variation in observed scores is caused by real differences in ability, and 20% of the variation is caused by errors in measurement--essentially, 20% of the variation in the test-takers’ scores is just noise and tells us nothing about students’ relative abilities.  Please refer to the first half of Methodologies for Evaluating the Validity of Scores Produced by CEFL’s Equivalency Exams for a more detailed exploration of reliability and validity.

Spearman-Brown Prophesy Formula

A test composed of more items produces results that have more reliability than the scores produced by shorter tests.  All items produce a signal and some noise.  The net signal indicated by the test scores tends to become more salient than the noise as more items are added.  This is because pure noise tends to cancel itself out and is not additive in the sense that noise plus noise usually equals about the same amount of noise, whereas signal plus signal typically results in more signal.  This holds as long as the items are in phase, i.e., each item tells us a little bit about a student’s ability in a certain subject matter.  Item analysis can tell show us which items are in phase and which are out of phase with the other items.  We can eliminate the out of phase items to boost the reliability of the test scores, or we can accept an out of phase item on the premise that many subject areas are not perfectly homogeneous, as long as the item tests something important.  In other words, certain items may march to the beat of their own drummer because the skills they legitimately test are largely unrelated to the other content in the course, which sometimes happens.

Increasing the number of items on a test usually increases validity because reliability sets the upper limit of validity.  Furthermore, more items usually means a greater variety of samples are taken from the content domain, thus increasing content validity.

Because our unit exams are shorter than diploma exams, we would expect them to produce less reliable results than diploma exams.  To be fair to our unit exams, we need a way of comparing apples to apples.  The Spearman-Brown Prophesy Formula foretells (prophesies) the reliability of an equivalent exam with a different length:

(Violato, 1992)

where L is the ratio of the number of items in the new test divided by the number of items in the original test; rxx is the reliability of the original exam; and r’ is the reliability of the new exam.

For instance, let us say that the reliability of the scores produced by a certain 24-item unit exam is 0.70, a respectable enough statistic in itself.  What would the reliability of the scores produced by a 40-item diploma exam be if it was constructed from items of the same quality as those used in the 24-item unit exam?  Given that the ratio, L, is 40/24 = 1.6 repeating and rxx=0.70, then:

Increasing the length of a 24-item exam by about 67% increases its reliability from 0.70 to 0.79.  This estimate is useful because it can help to answer the question “Is it worthwhile to lengthen this exam?  Is the improved precision of the results worth the temporal and monetary costs of a longer exam?  Could those temporal and monetary resources be better employed elsewhere?”  Of course, the answer is “it depends.”

The Reliability of Mathematics 30-1 Unit 1 Exam Form A (“Transformations and Functions”)

Since the Mathematics 30-1 unit exams were first implemented in Anytime Online, I have recorded the student scores (ID number, date, and score) for each exam.  Debbie Scott provided me with several student scores on the unit exams in Trad.  The following statistics are based on these data.  To estimate the reliability of a selected-response test, all we need are the students’ raw scores.  After one or two terms, we would usually have enough data.

The Mathematics 30-1 Unit 1 Exam Form A is out of 24 points.  Here are the relevant statistics based on 76 student records:

maximum possible raw score (k) = 24

standard deviation (s) = 4.72

mean (X) = 16.8 (70%)

The above statistics are easily calculated using a Google or Excel spreadsheet, or even a TI-84 calculator.

According to KR21, the reliability of the Mathematics 30-1 Unit 1 Exam Form A is:

A reliability coefficient of 0.81 is very good.  We can have some faith in this statistic because it is based on 76 student records.  But what if items of the same quality were used to construct a 40-item exam?  This hypothetical reliability can be prophesied thus:

If the Unit 1 Exam Form A was extended to 40 items, its reliability coefficient would be 0.87.  The reliability coefficient of the January 2013 Mathematics 30-1 diploma exam is estimated to be 0.90 by employing KR21.  Unit 1 Exam Form A compares very well to the Mathematics 30-1 diploma exam in terms of the reliability of the score set it produces.  This indicates that the items that compose the Unit 1 Exam are of a similar quality to the items that compose the diploma exam.

The Reliability of Mathematics 30-1 Unit 2 Exam Form A (“Trigonometry”)

The Mathematics 30-1 Unit 2 Exam Form A is out of 24 points.  Based on 48 student records from ATOL and Trad, here are the relevant statistics:

maximum possible raw score (k) = 24

standard deviation (s) = 5.59

mean (X) = 15.4 (64%)

According to KR21, the reliability of the Mathematics 30-1 Unit 2 Exam Form A is:

A reliability coefficient of 0.86 is impressive.  Let’s see what the coefficient would be if this exam was lengthened to 40 items: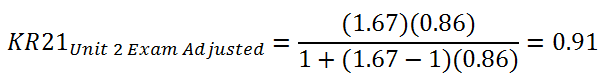

The reliability of a 40-item test composed of items of a similar quality as those used in Unit 2 Exam is prophesied to be 0.91.  The items that compose Unit 2 Exam are of a similar degree of quality as the items that compose the January 2013 Mathematics 30-1 diploma exam.

Spreadsheet for Easily Calculating Reliability Using KR21

Here’s a spreadsheet that you can copy that estimates the reliability of raw test scores that are recorded in column B: Reliability Estimator Employing KR21 .

The test scores in this spreadsheet are for illustration only.  Delete these scores and enter the raw scores for one of your own exams.  Note that if a student misses an exam and scores zero on that exam, then that score must NOT be entered because it would spuriously increase the reliability coefficient because it would spuriously increase the standard deviation; in other words, only the scores of bona fide test-takers are to be included.  Blank cells are ignored.

Conclusion and Next Steps

Mathematics 30-1 Unit 1 Exam Form A and Mathematics 30-1 Unit 2 Exam Form A produce results that can be relied upon.  Thus, in this respect, they are worthy of being cloned to produce version B exams.  These exams are composed of high-quality items in terms of the reliability of the results they produce.  Applying the Spearman-Brown Prophesy Formula allows us to compare the results produced by our unit exams to the longer diploma exams on an equal footing.

In a future article, I would like to discuss the limitations of the information provided by the reliability statistic.  Statistics can be used to aid in making predictions and evaluations; however, as always, “it depends.”

Regards,

Michael

Previous blog postings

References

Violato, C., McDougall, D., & Marini, A. (1992). Educational Measurement and Evaluation. Dubuque: Kendall/Hunt.